PageRank คืออะไร สำคัญอย่างไร

Google's PageRank คืออะไร? สำคัญอย่างไร?

แนวคิดของ PageRank

สวัสดีครับ เพื่อนๆ วันนี้ผมจะอธิบายถึง แนวคิดของ PageRank ว่ามีความสำคัญอย่างไร ครับอย่างที่รู้ๆกันสำหรับผู้ที่มีเว็บไชต์ ส่วนมากก็ต้องการที่จะ ทำให้เว็บเรา มีคนมาดูเยอะๆ ใช้ไหมครับ แต่จะทำอย่างไร ละ ก่อนอื่นต้อง รู้ก่อนว่า เว็บที่ให้บริการ สืบค้น อาทิเช่น Google ,Yahoo เขาต้องการข้อมูลอะไรจากเรา เรามีข้อมูลอะไร  หลักง่ายครับ ยกตัวอย่างหากผม ต้องการไปเที่ยวที่ใหนชักที่ ผมก็ต้องการ ข้อมูลสถานที่นั้นๆ ใช้ไหม ครับ แต่เราจะรู้ได้อย่างไรละ ก็ต้องสืบค้น ใช้ไหมครับ ข้อมูลที่เราสืบค้นต้องเป็นข้อมูลที่เราต้องการจริง ไม่ใช้ พบข้อมูลที่ เราต้องการ มาฟังกันครับ

           ตั้งแต่ขั้นเริ่มต้นของเวิลด์ไวด์เว็บ เครื่องมือที่ใช้ในการค้นหาข้อมูล มีความสำคัญมากเพราะข้อมูลต่างๆเหล่านั้นอยู่อย่างกระจัดกระจ่าย จำเป็นต้องมีเครื่องมือช่วย สืบค้นข้อมูล จึงได้มีกำเนิด เครื่องมือสืบค้นขี้นมาและได้มีการพัฒนาวิธีการที่แตกต่างกันในการจัดอันดับความสำคัญ ของหน้าเว็บ จนถึงการเกิดขึ้นของการค้นหา วลีภายในเอกสารซึ่ง ในเป็นปัจจัยที่สำคัญ ในเทคนิคการจัดอันดับของแทบเครื่องมือค้นหาใด ๆ การเกิดขึ้นของการค้นหาวลี จึงมีความสำคัญในการค้นหาขอมูล ดังนั้งจึงต้องให้ความสำคัญกับ ความยาวของเอกสาร (การจัดอันดับโดยใช้ความสำคัญของคำที่เราสืบค้น) หรือโดยการเน้น หัวข้อหลัก ภายในเอกสารโดยใช้ แท็ก (แท็ก เปรียบเสมือนกับสารบัญในหนังสือนั้นเองครับ)

       ฉนั้น หากเราได้ทำการ เขียนบทความหรือหนังสือชักเล่มเรา ก็ต้องรู้วัตถุประสงค์ที่เราจะสื่อสารอะไรออก ไปต้องการบอก อำไร กับใคร ที่ใหน อย่างไร และคนเหล่านั้นจะรู้ได้อย่างไร หาดูได้จากที่ไหน เข้าถึงข้อมูลนี้ได้อย่างไร ใช้ไหมละครับ          

1. Google PageRank คือวิธีการวัดความสำคัญของเว็บเพจนับล้าน ๆ เว็บเพจบนอินเตอร์เน็ท โดยมีตัวเลขตั้งแต่ 0 ถึง 10 ยิ่งตัวเลขยิ่งสูง PageRank ก็ยิ่งสูง นั่นหมายความว่าเว็บไซต์นั้นๆมีโอกาสได้รับการจัดอันดับที่ดีกว่าเว็บไซต์ที่มี PageRank ต่ำกว่า
โดยเราสามารถทราบค่า PR ของเว็บไซต์เราได้ โดย download และ install google toolbar (http://toolbar.google.com) หลังจากนั้นคุณจะสามารถดูคะแนน PR ของคุณที่จัดโดย google ได้
ถ้าไม่ต้องการ install google toolbar สามารถ check ค่า PageRank ได้ที่เว็บไซต์ www.pagerank.net
** หัวใจ ของ Page Rank คือ แลกลิงค์กับเว็บไซต์อื่นๆ ให้มาก และถ้าเป็นเว็บที่มีเนื้อหาเกี่ยวข้องกับเว็บเรา และ เป็นเว็บที่มีค่า PR สูง ยิ่งทำให้เว็บไซต์เรามีค่า PR สูงขึ้นด้วย

2. ค่า PR นั่นแสดงค่าทุกๆหน้าของเว็บไซต์เราใช่หรือไม่ ?
ค่า PR ของแต่ละเว็บเพจ ในเว็บไซต์หนึ่งๆ นั้นจะมีค่าแตกต่างกันไป ทั้งนี้ โดยมากโฮมเพจ มักมีค่า PR สูงกว่าหน้าอื่นๆ แต่ก็ไม่เสมอไป

3. Google คำนวณค่า PR อย่างไร ?
ค่า PR ถูกคำนวณ โดยจำนวนลิงก์ของเว็บไซต์อื่นๆ ที่เชื่อมลิงก์มายังเว็บไซต์ของคุณ (Inbound Link) ทั้งนี้คำนึงถึงคุณภาพ (คุณภาพของลิงก์หมายถึง เว็บเพจที่ลิงก์มาหาคุณมีความเกี่ยวข้องและเกี่ยวเนื่องกับเนื้อหาในเว็บไซต์ของคุณ ) และค่า PR ของเว็บไซต์ที่ลิงก์มายังเว็บไซต์คุณด้วย ยิ่งเว็บไซต์ที่ลิงก์มาหาคุณมี PR สูงๆ ค่า PR ของเว็บคุณก็มีแนวโน้มที่จะสูงตามไปด้วย ค่า PageRank นั้นใช้วิธีการเดียวกับระบบการโหวต หนึ่งลิงก์ที่เชื่อมโยงมายังเว็บไซต์ของคุณ ยิ่งมีค่า PR สูงเท่าใด Google ยิ่งเห็นความสำคัญของเว็บเพจนั้นๆมากยิ่งขึ้น และหากมีลิงก์มาจำนวนมากลิงก์มายังเว็บไซต์คุณ ค่า PR เว็บคุณก็จะสูงขึ้นตามไปด้วย

4. ทำอย่างไรถึงจะได้ค่า PR เพิ่มขึ้น ?
ค่า PR นั้นจะเพิ่มขึ้นได้ในแต่ละขั้นจาก 1 ไป 2 , จาก 2 ไป 3,... , จาก 9 ไป 10 นั้น มีกฏเกณฑ์ที่ค่อนข้างสลับซับซ้อน แต่ไม่ได้เป็นลักษณะเช่น คุณมีเว็บที่เชื่อมโยงลิงก์มาหาเว็บไซต์ คุณจาก 50 inbound link เป็น 100 inbound link (เพิ่มขึ้น 50 หน่วย) เว็บเพจนั้นๆอาจมีค่า PR เพิ่มขึ้นจาก 2 เป็น PR 3 แต่นั่นไม่ได้หมายความว่า ค่า PR 3 จะปรับเพิ่มขึ้นเป็น PR 4 โดย ที่คุณมี inbound link เพิ่มจาก 100 เป็น 150 (เพิ่มขึ้น 50 หน่วย) เสมอไป อาจต้องมี inbound link เพิ่มขึ้นถึง 200 หน่วย ค่า PR ถึงจะเพิ่มขึ้นก็เป็นได้ เพราะฉะนั้นในค่า PR ในแต่ละขั้นนั้น เป็นสิ่งที่ต้องอาศัยความรู้ ความพยายามเป็นอย่างมาก

5. การเพิ่มหน้าเว็บเพจที่มีเนื้อหาที่เป็นประโยชน์ส่งผลให้ค่า PR เพิ่มขึ้นหรือไม่ ?
คำตอบคือไม่ อย่างที่ได้กล่าวไปแล้วคือ หากคุณสามารถทำให้มีเว็บลิงก์มายังเว็บคุณได้มากขึ้นเท่าไหร่ PR ของเว็บคุณก็จะสูงมากขึ้นตามลำดับ แต่ทั้งนี้หากคุณนำเสนอเนื้อหาที่เป็นประโยชน์ในเว็บเพจนั้นๆ นั่นหมายความว่า คุณอาจได้รับการขอแลกลิงก์จากเว็บมาสเตอร์คนอื่นๆมายังเว็บไซต์คุณก็เป็นได้ ซึ่งเท่ากับเพิ่มจำนวนลิงก์ให้มากขึ้นในที่สุด

6. เนื้อหาของเว็บเพจที่ลิงก์มายังเว็บไซต์คุณ มีผลอย่างไรต่อค่า PR ?
หากเว็บเพจที่เชื่อมโยงลิงก์มายังเว็บคุณ มีเนื้อหาเกี่ยวเนื่องสัมพันธ์กับเว็บไซต์คุณมากเท่าใด Google จะพิจารณาให้ค่า PR ของเว็บคุณสูงยิ่งขึ้น

7. หากเว็บเพจที่เชื่อมโยงลิงก์มายังเว็บไซต์เรามี ค่า PR ต่ำ จะส่งผลกระทบต่อค่า PR ของเว็บไซต์เราหรือไม่ ?
การที่มีเว็บเพจเชื่อมโยงมาหาเว็บคุณจำนวนมากขึ้นนั้น โดยที่เว็บเพจนั้นๆมีค่า PR ระหว่าง 0-3 จะไม่ส่งผลกระทบต่อค่า PR ของเว็บคุณในทันที แต่เหมือนกับสะสมคะแนนไปเรื่อยๆ อย่างที่ได้กล่าวมาแล้ว ยิ่งเว็บเพจที่เชื่อมโยงมายังเว็บไซต์คุณมีเนื้อหาที่เกี่ยวเนื่องสัมพันธ์กับเว็บไซต์คุณมากเท่าใด ยังส่งผลดีมากกว่า เว็บเพจที่มีเนื้อหาที่ไม่ได้เกี่ยวข้องกับเว็บไซต์คุณเลยแต่มีค่า PR สูง และเชื่อมโยงลิงก์มาหาเว็บคุณ อย่าลืมว่า PageRank เป็นแค่ปัจจัยหนึ่งในการจัดลำดับความสำคัญของเว็บเพจหนึ่งๆเท่านั้น ยังมีปัจจัยอื่นๆอีกด้วย

8. เว็บที่มีค่า PR ต่ำๆ จะทำให้ค่า PR ของเว็บไซต์เรา ลดลงหรือไม่ ?
คำตอบคือ ไม่อย่างแน่นอน การแลกลิงก์กับเว็บไซต์ที่มีค่า PR ต่ำ (อาจเป็นเว็บที่เพิ่งเปิดตัว เป็นต้น) แต่มีเนื้อหาที่เกี่ยวพันกับเว็บไซต์คุณอาจทำให้ PR ของเว็บไซต์ของทั้งสองแห่งเพิ่มขึ้นพร้อมๆกันก็เป็นไปได้ แต่อย่าเข้าร่วมกับโปรแกรมแลกเปลี่ยนลิงก์ใดๆที่เป็นการโกงเสิร์ชเอนจิ้น ซึ่งจะทำให้เว็บไซต์คุณถูกถอนออกจากฐานข้อมูลของเสิร์ชเอนจิ้นในทีสุด

9. ค่า PR เราตกลงได้หรือไม่ ?
ค่า PageRank สามารถลดลงได้ หากเว็บไซต์คุณมีจำนวนลิงก์ที่เชื่อมโยงมาหาเว็บไซต์คุณน้อยลง ซึ่งบางครั้งอาจเกิดขึ้นจากเว็บไซต์ที่เชื่อมโยงมาหาคุณมีค่า PR ลดลงก็เป็นได้





The PageRank Algorithm

The original PageRank algorithm was described by Lawrence Page and Sergey Brin in several publications. It is given by
PR(A) = (1-d) + d (PR(T1)/C(T1) + ... + PR(Tn)/C(Tn))
where

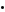	PR(A) is the PageRank of page A,
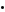	PR(Ti) is the PageRank of pages Ti which link to page A,
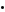	C(Ti) is the number of outbound links on page Ti and
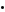	d is a damping factor which can be set between 0 and 1.

So, first of all, we see that PageRank does not rank web sites as a whole, but is determined for each page individually. Further, the PageRank of page A is recursively defined by the PageRanks of those pages which link to page A.
The PageRank of pages Ti which link to page A does not influence the PageRank of page A uniformly. Within the PageRank algorithm, the PageRank of a page T is always weighted by the number of outbound links C(T) on page T. This means that the more outbound links a page T has, the less will page A benefit from a link to it on page T.
The weighted PageRank of pages Ti is then added up. The outcome of this is that an additional inbound link for page A will always increase page A's PageRank.
Finally, the sum of the weighted PageRanks of all pages Ti is multiplied with a damping factor d which can be set between 0 and 1. Thereby, the extend of PageRank benefit for a page by another page linking to it is reduced.

The Random Surfer Model

In their publications, Lawrence Page and Sergey Brin give a very simple intuitive justification for the PageRank algorithm. They consider PageRank as a model of user behaviour, where a surfer clicks on links at random with no regard towards content.
The random surfer visits a web page with a certain probability which derives from the page's PageRank. The probability that the random surfer clicks on one link is solely given by the number of links on that page. This is why one page's PageRank is not completely passed on to a page it links to, but is devided by the number of links on the page.
So, the probability for the random surfer reaching one page is the sum of probabilities for the random surfer following links to this page. Now, this probability is reduced by the damping factor d. The justification within the Random Surfer Model, therefore, is that the surfer does not click on an infinite number of links, but gets bored sometimes and jumps to another page at random.
The probability for the random surfer not stopping to click on links is given by the damping factor d, which is, depending on the degree of probability therefore, set between 0 and 1. The higher d is, the more likely will the random surfer keep clicking links. Since the surfer jumps to another page at random after he stopped clicking links, the probability therefore is implemented as a constant (1-d) into the algorithm. Regardless of inbound links, the probability for the random surfer jumping to a page is always (1-d), so a page has always a minimum PageRank.

A Different Notation of the PageRank Algorithm

Lawrence Page and Sergey Brin have published two different versions of their PageRank algorithm in different papers. In the second version of the algorithm, the PageRank of page A is given as
PR(A) = (1-d) / N + d (PR(T1)/C(T1) + ... + PR(Tn)/C(Tn))
where N is the total number of all pages on the web. The second version of the algorithm, indeed, does not differ fundamentally from the first one. Regarding the Random Surfer Model, the second version's PageRank of a page is the actual probability for a surfer reaching that page after clicking on many links. The PageRanks then form a probability distribution over web pages, so the sum of all pages' PageRanks will be one.
Contrary, in the first version of the algorithm the probability for the random surfer reaching a page is weighted by the total number of web pages. So, in this version PageRank is an expected value for the random surfer visiting a page, when he restarts this procedure as often as the web has pages. If the web had 100 pages and a page had a PageRank value of 2, the random surfer would reach that page in an average twice if he restarts 100 times.
As mentioned above, the two versions of the algorithm do not differ fundamentally from each other. A PageRank which has been calculated by using the second version of the algorithm has to be multiplied by the total number of web pages to get the according PageRank that would have been caculated by using the first version. Even Page and Brin mixed up the two algorithm versions in their most popular paper "The Anatomy of a Large-Scale Hypertextual Web Search Engine", where they claim the first version of the algorithm to form a probability distribution over web pages with the sum of all pages' PageRanks being one.
In the following, we will use the first version of the algorithm. The reason is that PageRank calculations by means of this algorithm are easier to compute, because we can disregard the total number of web pages.

The Characteristics of PageRank

The characteristics of PageRank shall be illustrated by a small example.

We regard a small web consisting of three pages A, B and C, whereby page A links to the pages B and C, page B links to page C and page C links to page A. According to Page and Brin, the damping factor d is usually set to 0.85, but to keep the calculation simple we set it to 0.5. The exact value of the damping factor d admittedly has effects on PageRank, but it does not influence the fundamental principles of PageRank. So, we get the following equations for the PageRank calculation:


PR(A) = 0.5 + 0.5 PR(C)
PR(B) = 0.5 + 0.5 (PR(A) / 2)
PR(C) = 0.5 + 0.5 (PR(A) / 2 + PR(B))
These equations can easily be solved. We get the following PageRank values for the single pages:
PR(A) = 14/13 = 1.07692308
PR(B) = 10/13 = 0.76923077
PR(C) = 15/13 = 1.15384615
It is obvious that the sum of all pages' PageRanks is 3 and thus equals the total number of web pages. As shown above this is not a specific result for our simple example.
For our simple three-page example it is easy to solve the according equation system to determine PageRank values. In practice, the web consists of billions of documents and it is not possible to find a solution by inspection.

The Iterative Computation of PageRank

Because of the size of the actual web, the Google search engine uses an approximative, iterative computation of PageRank values. This means that each page is assigned an initial starting value and the PageRanks of all pages are then calculated in several computation circles based on the equations determined by the PageRank algorithm. The iterative calculation shall again be illustrated by our three-page example, whereby each page is assigned a starting PageRank value of 1.

Iteration	PR(A)	PR(B)	PR(C)
0	1	1	1
1	1	0.75	1.125
2	1.0625	0.765625	1.1484375
3	1.07421875	0.76855469	1.15283203
4	1.07641602	0.76910400	1.15365601
5	1.07682800	0.76920700	1.15381050
6	1.07690525	0.76922631	1.15383947
7	1.07691973	0.76922993	1.15384490
8	1.07692245	0.76923061	1.15384592
9	1.07692296	0.76923074	1.15384611
10	1.07692305	0.76923076	1.15384615
11	1.07692307	0.76923077	1.15384615
12	1.07692308	0.76923077	1.15384615

We see that we get a good approximation of the real PageRank values after only a few iterations. According to publications of Lawrence Page and Sergey Brin, about 100 iterations are necessary to get a good approximation of the PageRank values of the whole web.
Also, by means of the iterative calculation, the sum of all pages' PageRanks still converges to the total number of web pages. So the average PageRank of a web page is 1. The minimum PageRank of a page is given by (1-d). Therefore, there is a maximum PageRank for a page which is given by dN+(1-d), where N is total number of web pages. This maximum can theoretically occur, if all web pages solely link to one page, and this page also solely links to itself.

By kongnakornseo